研究
鱼群的控制
鱼群的典型数学模型涉及吸引/对齐/排斥定律，这在当前的系统和控制理论中不一定得到充分考虑。 在我们的研究项目中，我们正在开发分析和控制鱼群模型的理论。
参考文献
| [2] | M. Ogura and N. Wakamiya, “Reduced-order model predictive control of a fish schooling model,” Nonlinear Analysis: Hybrid Systems, vol. 49, p. 101342, 2023. [ DOI | arXiv | http ] |
| [1] | M. Ogura and N. Wakamiya, “Model predictive control of fish schooling model with reduced-order prediction model,” in 60th IEEE Conference on Decision and Control, 2021, pp. 4115-4120. [ DOI | http ] |
放牧
牧羊问题是指通过较少的外部实体将另一群实体从初始位置引导到目标位置的问题，并且具有一些潜在的应用，例如机器人放羊和人群控制。 我们正在开发用于引导异构代理的新算法。
提案法
最远主体定位法
参考文献
| [12] | W. Imahayashi, Y. Tsunoda, and M. Ogura, “Route design in sheepdog system–traveling salesman problem formulation and evolutionary computation solution–,” Advanced Robotics, vol. 38, no. 9-10, pp. 632-646, 2024. [ DOI | arXiv | http ] |
| [11] | Y. Deng, A. Li, M. Ogura, and N. Wakamiya, “Collision-free shepherding control of a single target within a swarm,” in 2023 IEEE International Conference on Systems, Man, and Cybernetics, 2023, pp. 5218-5223. [ DOI | arXiv | http ] |
| [10] | A. Fujioka, M. Ogura, and N. Wakamiya, “Shepherding heterogeneous flocks: overview and prospect,” in 22nd IFAC World Congress, 2023, pp. 11523-11526. [ arXiv ] |
| [9] | Y. Deng, A. Li, M. Ogura, and N. Wakamiya, “Collision-free property analysis for the shepherding swarm,” in SICE Annual Conference 2023, 2023, pp. 1072-1073. |
| [8] | A. Li, M. Ogura, and N. Wakamiya, “Communication-free shepherding navigation with multiple steering agents,” Frontiers in Control Engineering, vol. 4, 2023. [ DOI | arXiv | http ] |
| [7] | A. Fujioka, M. Ogura, and N. Wakamiya, “Shepherding algorithm for heterogeneous flock with model-based discrimination,” Advanced Robotics, vol. 37, no. 1-2, pp. 99-114, 2023. [ DOI | arXiv | http ] |
| [6] | A. Li, M. Ogura, and N. Wakamiya, “Proposal of a bearing-only shepherding algorithm with limited sensing capabilities,” in AROB-ISBC-SWARM 2023, 2023, pp. GS34-1. |
| [5] | Y. Deng, M. Ogura, A. Li, and N. Wakamiya, “Shepherding control for separating a single agent from a swarm,” in 1st IFAC Workshop on Control of Complex Systems, 2022, pp. 217-222. [ DOI | arXiv | http ] |
| [4] | A. Fujioka, M. Ogura, and N. Wakamiya, “Shepherding algorithm based on variant agent detection for heterogeneous flock,” in SICE Annual Conference 2022, 2022, pp. 87-91. Finalists of SICE Annual Conference 2022 Young Author's Award. [ DOI | http ] |
| [3] | A. Li, M. Ogura, Y. Tsunoda, and N. Wakamiya, “Proposal of farthest-agent targeting algorithm with indirect chasing,” in SICE Annual Conference 2022, 2022, pp. 92-94. |
| [2] | R. Himo, M. Ogura, and N. Wakamiya, “Iterative algorithm for shepherding unresponsive sheep,” Mathematical Biosciences and Engineering, vol. 19, no. 4, pp. 3509-3525, 2022. [ DOI | http ] |
| [1] | R. Himo, M. Ogura, and N. Wakamiya, “Shepherding algorithm for agents with heterogeneous sensitivities,” in 4th International Symposium on Swarm Behavior and Bio-Inspired Robotics 2021, 2021. [ http ] |
基于模型控制的深度展开 (TAF，CREST）
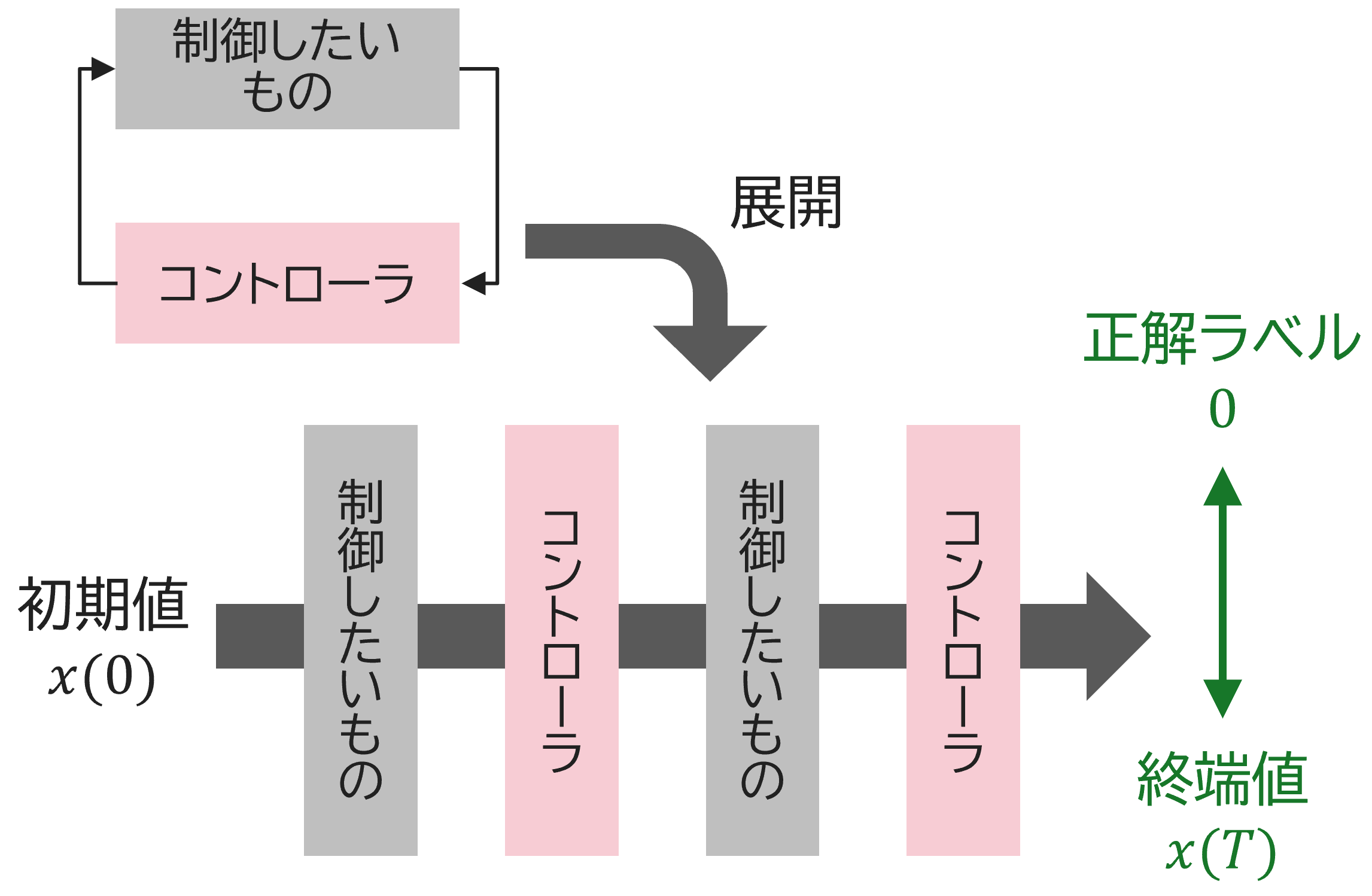
我们正在利用称为深度展开的新型机器学习技术开发基于模型的控制器合成框架。 我们发现我们的方法对于控制各种类型的动态系统非常有效，这包括饱和系统、延迟系统和随机噪声系统。
参考文献
| [10] | J. Aizawa, M. Ogura, M. Shimono, and N. Wakamiya, “Firing pattern manipulation of neuronal networks by deep unfolding‐based model predictive control,” IET Control Theory & Applications, vol. 18, no. 15, pp. 2003-2013, 2024. [ DOI | http ] |
| [9] | J. J. R. Liu, M. Ogura, Q. Li, and J. Lam, “Learning-based stabilization of Markov jump linear systems,” Neurocomputing, vol. 584, p. 127618, 2024. [ DOI | http ] |
| [8] | J. Aizawa, M. Ogura, M. Shimono, and N. Wakamiya, “Manipulation of neuronal network firing patterns using temporal deep unfolding-based MPC,” in 2023 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, 2023, pp. 15-21. [ DOI | arXiv | http ] |
| [7] | “Enhancing Control System Design through Deep Unfolding: A Systematic Approach,” University of Hawaii at Manoa, 2023. [ http ] |
| [6] | J. Aizawa, M. Ogura, M. Shimono, and N. Wakamiya, “Temporal deep unfolding-based MPC for controlling firing patterns of neuronal network,” in 2023 RISP International Workshop on Nonlinear Circuits, Communications and Signal Processing, 2023. |
| [5] | M. Ogura, K. Kobayashi, and K. Sugimoto, “Static output feedback synthesis of time-delay linear systems via deep unfolding,” in 17th IFAC Workshop on Time Delay Systems, 2022, pp. 214-215. [ arXiv ] |
| [4] | “When deep unfolding meets control engineering,” 37th International Technical Conference on CircuitsSystems, Computers and Communications, 2022. [ http ] |
| [3] | M. Kishida and M. Ogura, “Temporal deep unfolding for nonlinear maximum hands-off control,” in SICE Annual Conference 2021, 2021, pp. 1007-1010. [ arXiv ] |
| [2] | K. Kobayashi, M. Ogura, T. Kobayashi, and K. Sugimoto, “Deep unfolding-based output feedback control design for linear systems with input saturation,” in SICE International Symposium on Control Systems 2021, 2021, pp. 33-39. [ DOI | arXiv | http ] |
| [1] | M. Kishida*, M. Ogura*, Y. Yoshida, and T. Wadayama, “Deep learning-based average consensus,” IEEE Access, vol. 8, pp. 142404-142412, 2020. (*equal contribution) [ DOI | arXiv | http ] |
社交网络中的流行病控制 (JSPS Grant-in-Aid for Early-Career Scientists)
由于当前的 COIVD-19 大流行，控制社交网络中发生的流行过程是一个具有理论和实践意义的关键问题。 由于疫苗尚未完全可用（截至 2021 年 3 月 16 日），我们仍然需要依靠保持社交距离。 这种社交距离策略可以被视为对流行过程的反馈控制，因为社交距离的程度与疾病的传播呈正相关。 在我们的研究小组中，我们正在利用系统和控制理论来开发新的理论框架，以预测和遏制复杂网络上的流行病传播过程。
幻灯片
参考文献
| [8] | R. Liu, M. Ogura, E. F. Dos Reis, and N. Masuda, “Effects of concurrency on epidemic spreading in Markovian temporal networks,” European Journal of Applied Mathematics, vol. 35, no. 3, pp. 430-461, 2024. [ DOI | arXiv | http ] |
| [7] | M. Ogura and C. Nowzari, “Special issue: modeling, analysis, and control of epidemics in networks,” Mathematical Biosciences and Engineering, vol. 20, no. 5, pp. 8446-8447, 2023. [ DOI | http ] |
| [6] | K. Hashimoto, Y. Onoue, M. Ogura, and T. Ushio, “Event-triggered control for mitigating SIS spreading processes,” Annual Reviews in Control, vol. 52, pp. 479-494, 2021. [ DOI | arXiv | http ] |
| [5] | N. Masuda, V. M. Preciado, and M. Ogura, “Analysis of the susceptible-infected-susceptible epidemic dynamics in networks via the non-backtracking matrix,” IMA Journal of Applied Mathematics, vol. 85, no. 2, pp. 214-230, 2020. [ arXiv | http ] |
| [4] | M. Ogura, W. Mei, and K. Sugimoto, “Upper-bounding dynamics on networked synergistic susceptible-infected-susceptible model,” in SICE Annual Conference 2019, 2019, pp. 1430-1431. |
| [3] | M. Ogura, V. M. Preciado, and N. Masuda, “Optimal containment of epidemics over temporal activity-driven networks,” SIAM Journal on Applied Mathematics, vol. 79, no. 3, pp. 986-1006, 2019. [ DOI | arXiv | http ] |
| [2] | M. Ogura and V. M. Preciado, “Second-order moment-closure for tighter epidemic thresholds,” Systems & Control Letters, vol. 113, pp. 59-64, 2018. [ DOI | arXiv | http ] |
| [1] | M. Ogura and V. M. Preciado, “Stability of spreading processes over time-varying large-scale networks,” IEEE Transactions on Network Science and Engineering, vol. 3, no. 1, pp. 44-57, 2016. Runner-up of 2019 IEEE TNSE Best Paper Award. [ DOI | arXiv | http ] |
正向系统（NII Open Collaborative Research）
正系统，粗略地说，是一类动力系统，其对非负输入信号的响应信号被限制为非负，并且在药理学、流行病学、人口生物学和通信网络等各个领域都有应用。 在我们的研究小组中，我们正在开发一种新颖的数学框架，用于使用几何规划优化正系统。 该框架适用于几个具有理论意义的问题，例如 H2 和 H-infinity 优化以及时延和结构化不确定性下的优化。
幻灯片
参考文献
| [9] | C. Zhao, K. Sakurama, and M. Ogura, “Optimal toll strategy for traffic flow network: A geometric programming approach,” Under preparation, 2024. |
| [8] | C. Zhao, B. Zhu, M. Ogura, and J. Lam, “Probability rate optimization of positive Markov jump linear systems via DC programming,” Asian Journal of Control (accepted for publication), 2024. [ DOI ] |
| [7] | C. Zhao, B. Zhu, M. Ogura, and J. Lam, “Parameterized synthesis of discrete-time positive linear systems: A geometric programming perspective,” IEEE Control Systems Letters, vol. 7, pp. 2551-2556, 2023. [ DOI | http ] |
| [6] | C. Zhao, X. Gong, Y. Ebihara, and M. Ogura, “Impulse-to-peak optimization of positive linear systems via DC programming,” in 22nd IFAC World Congress, 2023, pp. 5544-5549. [ DOI | http ] |
| [5] | X. Gong, M. Ogura, J. Shen, T. Huang, and Y. Cui, “Optimal epidemics policy seeking on networks-of-networks under malicious attacks by geometric programming,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 53, no. 6, pp. 3845-3857, 2023. [ DOI | http ] |
| [4] | B. Zhu, J. Lam, and M. Ogura, “Log-log convexity of an optimal control problem for positive linear systems,” Automatica, vol. 146, p. 110553, 2022. [ DOI | http ] |
| [3] | M. Ogura, M. Kishida, and J. Lam, “Geometric programming for optimal positive linear systems,” IEEE Transactions on Automatic Control, vol. 65, no. 11, pp. 4648-4663, 2020. [ DOI | arXiv | http ] |
| [2] | C. Zhao, M. Ogura, and K. Sugimoto, “Stability optimization of positive semi-Markov jump linear systems via convex optimization,” SICE Journal of Control, Measurement, and System Integration, vol. 13, no. 5, pp. 233-239, 2020. [ DOI | arXiv | http ] |
| [1] | M. Ogura and C. F. Martin, “Stability analysis of positive semi-Markovian jump linear systems with state resets,” SIAM Journal on Control and Optimization, vol. 52, pp. 1809-1831, 2014. [ DOI | arXiv | http ] |
控制理论与设计工程相遇（NII Open Collaboration Research）
在大多数行业中，项目对于执行多种类型的工作是必不可少且核心的（PMI 2013）。 因此，项目管理一直是近半个世纪以来工程设计领域的主要研究课题之一。 在我们的研究项目中，通过利用系统和控制理论中关于正系统和切换系统的理论结果，我们正在开发一个优化框架来进行经济高效的投资，其在模块之间的底层依赖结构随时间变化而变化。
幻灯片
参考文献
| [2] | C. Zhao, M. Ogura, M. Kishida, and A. Yassine, “Optimal resource allocation for dynamic product development process via convex optimization,” Research in Engineering Design, vol. 32, no. 1, pp. 71-90, 2021. [ DOI | arXiv | http ] |
| [1] | M. Ogura, J. Harada, M. Kishida, and A. Yassine, “Resource optimization of product development projects with time-varying dependency structure,” Research in Engineering Design, vol. 30, no. 3, pp. 435-452, 2019. [ DOI | arXiv | http ] |